Un nou model permet recrear lʼarbre genealògic de les xarxes complexes
En un nou estudi publicat a Proceedings of the National Academy of Sciences (PNAS), un equip de recerca de lʼInstitut de Sistemes Complexos de la UB (UBICS) ha analitzat lʼevolució temporal de xarxes complexes reals i ha desenvolupat un model en el qual lʼaparició de nous nodes es pot relacionar amb nodes preexistents, dʼuna manera similar a lʼevolució de les espècies en biologia.

En un nou estudi publicat a Proceedings of the National Academy of Sciences (PNAS), un equip de recerca de lʼInstitut de Sistemes Complexos de la UB (UBICS) ha analitzat lʼevolució temporal de xarxes complexes reals i ha desenvolupat un model en el qual lʼaparició de nous nodes es pot relacionar amb nodes preexistents, dʼuna manera similar a lʼevolució de les espècies en biologia.
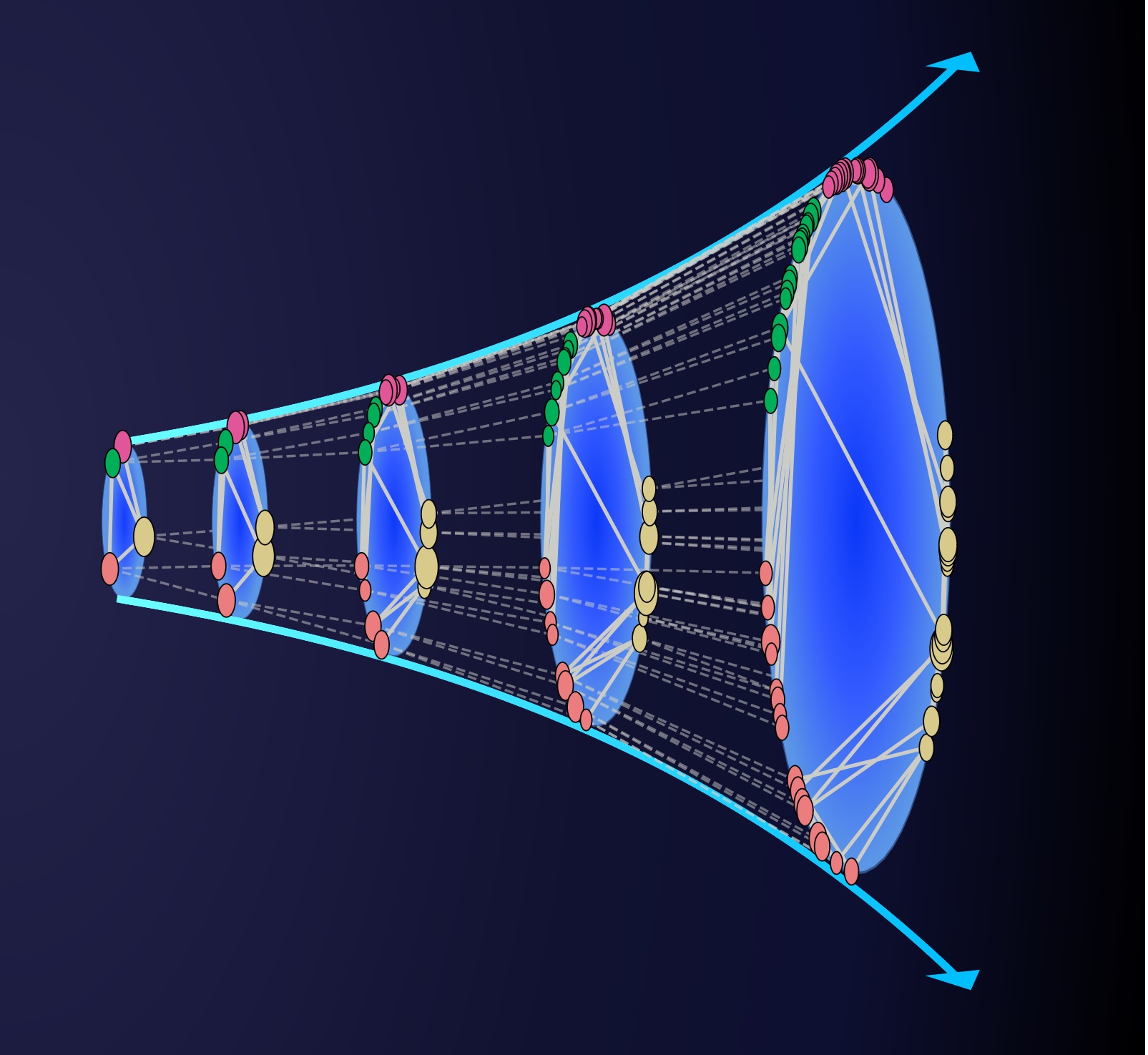
En aquest estudi sʼanalitza lʼevolució temporal de la xarxa de citacions en revistes científiques i la xarxa de comerç internacional al llarg dʼun període de més de cent anys. Segons explica M. Ángeles Serrano, investigadora ICREA a lʼUBICS, «el que sʼobserva en aquestes xarxes reals és que totes dues creixen dʼuna manera autosimilar, és a dir, les seves propietats de connectivitat es mantenen invariables al llarg del temps, així que lʼestructura de la xarxa és sempre la mateixa, mentre que el nombre de nodes va augmentant».
Aquesta autosimilitud en el creixement, ja de per si sorprenent, els investigadors lʼhan pogut explicar a partir dʼun model anomenat creixement de ramificació geomètrica (geometric branching growth o GBG). En aquest model, els nous nodes provenen de nodes preexistents, dʼuna manera similar als arbres genealògics. Per exemple, en la xarxa de comerç mundial, els països són els nodes, i per tant els que es bifurquen, i les transaccions corresponen als enllaços. La propietat clau que caracteritza lʼevolució dels sistemes en estudi, i per tant el model, és lʼherència. En lʼexemple, quan un país es divideix, els nous països sobirans hereten la riquesa i els socis comercials de lʼestat original.
Aquest model està relacionat amb un treball anterior que permetia produir versions reduïdes autosimilars de xarxes complexes, mitjançant un procés de renormalització geomètrica. En aquests treballs anteriors, es va trobar que la connectivitat en les xarxes complexes a diferents escales espacials es regula pels mateixos principis. «El que veiem en el nou article —destaca la investigadora— és que aquests mateixos principis es mantenen també al llarg del temps».
Quan es combinen els dos models —el GBG i la renormalització geomètrica—, es poden crear rèpliques de la xarxa original en una gamma molt àmplia de mides, més grans o més petites que lʼoriginal. «Dʼaquesta manera, es podrien predir nodes descendents o nodes ascendents, o estudiar fenòmens que depenen de la mida de la xarxa», remarca Serrano. «Les xarxes presenten, doncs, una estructura fractal en lʼespai i el temps», afegeix.
Aquests processos de ramificació són la base de lʼevolució complexa de molts sistemes reals. «En resum, els dos models permeten entendre les interaccions en sistemes reals a diferents escales, una de les claus per entendre i predir com serà la seva evolució», conclou lʼexperta.
Referència de lʼarticle
Muhua Zheng, Guillermo García-Pérez, Marián Boguñá, i M. Ángeles Serrano. «Scaling up real networks by geometric branchinggrowth», Proceedings of the National Academy of Sciences, maig de 2021. DOI: 10.1073/pnas.2018994118