Un nou mètode permet determinar la dimensionalitat de les xarxes complexes mitjançant la geometria hiperbòlica
Reduir informació redundant per trobar patrons simplificadors en conjunts de dades i xarxes complexes és un repte científic en molts àmbits del coneixement. A més, detectar la dimensionalitat de les dades és encara un problema de difícil resolució. Ara, un article publicat a la revista Nature Communications presenta un mètode per inferir la dimensionalitat de les xarxes complexes aplicant la geometria hiperbòlica, que captura la complexitat de les estructures relacionals del món real en dominis molt diversos.

Reduir informació redundant per trobar patrons simplificadors en conjunts de dades i xarxes complexes és un repte científic en molts àmbits del coneixement. A més, detectar la dimensionalitat de les dades és encara un problema de difícil resolució. Ara, un article publicat a la revista Nature Communications presenta un mètode per inferir la dimensionalitat de les xarxes complexes aplicant la geometria hiperbòlica, que captura la complexitat de les estructures relacionals del món real en dominis molt diversos.
Són autors dʼaquest nou treball els investigadors M. Ángeles Serrano i Marián Boguñá, de la Facultat de Física i lʼInstitut de Sistemes Complexos de la UB (UBICS), i Pedro Almagro, de lʼEscola Tècnica Superior dʼEnginyeria Informàtica de la Universitat de Sevilla. La recerca aporta un model hiperbòlic multidimensional de xarxes complexes que en reprodueix fidelment la connectivitat, amb una dimensionalitat ultra baixa i personalitzable per a cada xarxa concreta. Això permet caracteritzar-ne millor lʼestructura —per exemple, a escala de comunitats— i millorar la seva capacitat predictiva.
Lʼestudi revela regularitats inesperades, com ara que les dimensions de les xarxes moleculars associades a teixits biològics són extremament baixes; que la dimensionalitat que exigeixen les xarxes socials i Internet és lleugerament superior, i que els connectomes cerebrals estan a prop de les tres dimensions de la seva organització anatòmica.
Geometria hiperbòlica versus euclidiana
La geometria intrínseca dels conjunts de dades o de les xarxes complexes no és òbvia, la qual cosa és un obstacle a lʼhora de determinar la dimensionalitat de les xarxes reals. Un altre desafiament és que la distància sʼha de definir dʼacord amb la seva estructura relacional i de connectivitat, i això també requereix models sofisticats.
Ara, el nou enfocament té com a referència la geometria de les xarxes complexes; més en concret, el model geomètric configuracional o model SD. «Aquest model, que hem desenvolupat en treballs anteriors, descriu lʼestructura de les xarxes complexes basant-se en principis fonamentals», explica la professora M. Ángeles Serrano, que és investigadora ICREA del Departament de Física de la Matèria Condensada de la UB.
«Més específicament —continua—, el model postula una llei dʼinterconnexió dels elements de la xarxa (o nodes) que és de tipus gravitatori, de manera que nodes més propers en un espai de similitud (de geometria esfèrica en D dimensions) i amb més popularitat (una dimensió extra que correspon a la importància del node) tenen més probabilitats dʼestablir connexions».
En lʼestudi, les variables de similitud i de popularitat es combinen per donar lloc a la geometria hiperbòlica del model, que emergeix com la geometria natural que representa lʼarquitectura jeràrquica de les xarxes complexes.
En treballs previs, lʼequip havia aplicat la versió més simple del model SD en una dimensió —el model S1— per tal dʼexplicar moltes de les característiques típiques de les xarxes del món real: la propietat de món petit (els sis graus de separació); les distribucions heterogènies del nombre de veïns per nodes, i els alts nivells de relacions transitives (connexions en triangle que es poden il·lustrar amb la frase «lʼamic del meu amic és també el meu amic»).
«A més, lʼaplicació de tècniques dʼinferència estadística ens permet obtenir mapes de xarxes reals en el pla hiperbòlic que són congruents amb el model establert», destaca la investigadora. «Més enllà de la visualització, aquestes representacions sʼhan utilitzat en multitud de tasques que inclouen els mètodes de navegació eficient, la detecció de patrons dʼautosemblança, la detecció de comunitats de nodes fortament interactius i la implementació dʼun procediment de renormalització de xarxes que evidencia simetries ocultes en lʼorganització multiescalar de les xarxes complexes i que permet produir rèpliques de la xarxa a escala reduïda o augmentada».
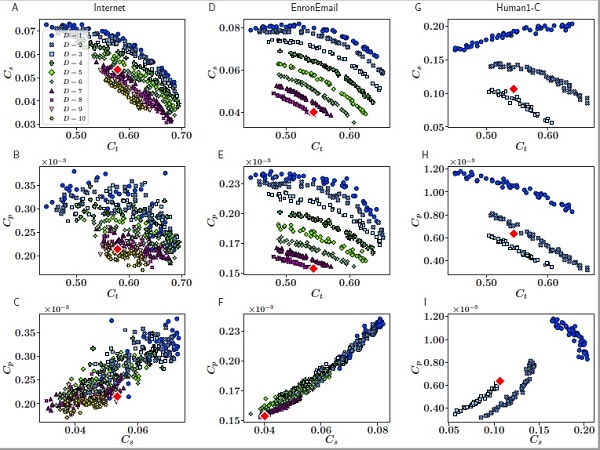
Ara, lʼequip infereix quina és la dimensionalitat de lʼespai hiperbòlic subjacent a les xarxes reals a partir de propietats que es relacionen amb la dimensió de la seva geometria. En particular, el treball mesura lʼestadística de cicles dʼordre superior (triangles, quadrats, pentàgons) associats a les connexions.
Una metodologia aplicable a totes les xarxes complexes
En ciències de la computació, les tècniques aplicades es basen en dades que sovint fan servir definicions de distància de similitud entre els elements. Aquest enfocament implica construir grafs que es cartografien en un espai latent de característiques euclidianes.
«Les nostres estimacions de la dimensionalitat de les xarxes complexes estan molt per sota de les estimacions basades en lʼespai euclidià, ja que lʼespai hiperbòlic és més adient per representar lʼestructura jeràrquica de xarxes complexes reals. Per exemple, Internet només requereix D = 7 dimensions per ser mapejat en lʼespai hiperbòlic del nostre model, mentre que aquest nombre es multiplica per sis i escala fins a D = 47 en una de les tècniques més recents que fan servir lʼespai euclidià», detalla el catedràtic Marián Boguñá.
A més, les tècniques per mapejar dades complexes sovint suposen un espai latent, amb un nombre predeterminat de dimensions, o bé implementen tècniques heurístiques per trobar-ne un valor adequat. Així, el nou mètode es basa en un model que no necessita el mapejat espacial de la xarxa per tal de determinar la dimensió de la seva geometria.
En el camp de la ciència de xarxes, moltes metodologies fan servir les distàncies més curtes per estudiar lʼestructura de connectivitat de la xarxa (shortest paths) com a espai mètric. Ara bé, aquestes distàncies es veuen fortament afectades per la propietat de món petit i no proporcionen un rang ampli de valors de distància.
«El nostre model fa servir una definició de distància completament diferent i basada en un espai hiperbòlic subjacent, i no necessitem mapejar la xarxa. La nostra metodologia és aplicable a qualsevol xarxa real o conjunt de dades amb una estructura complexa i amb una mida que típicament és de milers o desenes de milers de nodes, però que pot arribar a centenars de milers en un temps raonable de computació», subratlla M. Ángeles Serrano.
Quina és la dimensionalitat real de les xarxes socials i Internet?
Les conclusions apunten que la dimensió de les xarxes socials i Internet és entre 6 i 9 vegades més alta que la de xarxes dʼaltres àmbits. Ara bé, encara és 6 o 7 vegades més baixa que lʼobtinguda amb altres mètodes. Això mostra que les interaccions en aquests sistemes són més complexes i estan determinades per una varietat més gran de factors.
Per la seva banda, les xarxes socials basades en amistat són al capdavant del rànquing de dimensionalitat. «És un resultat inesperat, ja que en principi es podria pensar que lʼamistat és un tipus de relació afectiva més lliure. Però els nostres resultats lliguen amb el fet que lʼhomofília en les interaccions humanes està determinada per nombrosos factors sociològics, com ara lʼedat, el sexe, la classe social, les creences, les actituds o els interessos», apunta Serrano.
En el cas dʼInternet, tot i ser una xarxa tecnològica, la seva gran dimensionalitat és un reflex del fet que, per a un sistema autònom, connectar-se no vol dir només accedir al sistema (com es podria pensar a priori), sinó que en la formació dʼaquestes connexions hi influeixen molts factors diferents. Com a conseqüència, hi poden ser presents moltes relacions ben diverses, com ara proveïdor-client, dʼigual a igual (peer-to-peer), intercanvi entre iguals (peering exchange), etc.
«El que és realment sorprenent, tant per a les xarxes socials com per a Internet, és que el nostre marc teòric —que no fa servir cap anotació sobre les connexions més enllà de la seva existència— sigui capaç de captar aquesta realitat multidimensional que no és explícita en les nostres dades», conclou lʼequip, que actualment treballa per construir mapes multidimensionals hiperbòlics de les xarxes complexes que siguin congruents amb el marc teòric establert pel model SD.
Article de referència:
Almagro, P.; Boguñá, M.; Serrano, M. A. «Detecting the ultra low dimensionality of real networks». Nature Communications, octubre de 2022. DOI: 10.1038/s41467-022-33685-z