A new model enables the recreation of the family tree of complex networks
In a new study published in Proceedings of the National Academy of Sciences (PNAS), a research team of the Institute of Complex Systems of the UB (UBICS) analysed the time evolution of real complex networks and developed a model in which the emergence of new nodes can be related to pre-existing nodes, similarly to the evolution of species in biology.

In a new study published in Proceedings of the National Academy of Sciences (PNAS), a research team of the Institute of Complex Systems of the UB (UBICS) analysed the time evolution of real complex networks and developed a model in which the emergence of new nodes can be related to pre-existing nodes, similarly to the evolution of species in biology.
This new study analyses the time evolution of the citation network in scientific journals and the international trade network over a 100-year period. According to M. Ángeles Serrano, ICREA researcher at UBICS, “what we observe in these real networks is that both grow in a self-similar way, that is, their connectivity properties remain invariable over time, so that the network structure is always the same, while the number of nodes increases”.
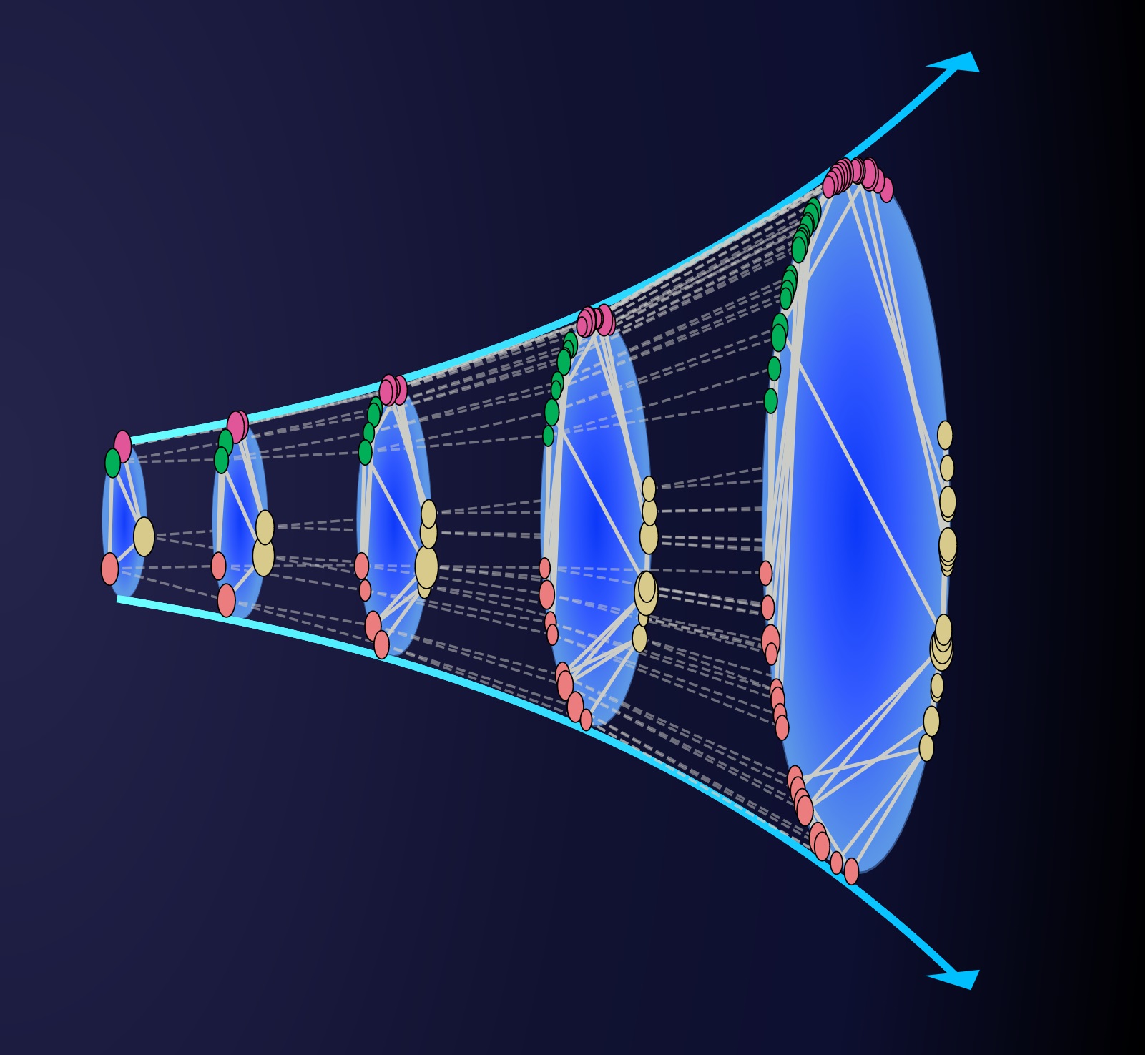
This self-similarity in growth, which is surprising per se, has been explained by the researchers using a model named geometric branching growth (GBG). In this model, the new nodes come from pre-existing nodes, in a similar way to family trees. For instance, in the world trade network, countries are nodes, and therefore they branch off, and transactions correspond to the links. The key property that characterizes the evolution of systems in study, and therefore the model, is inheritance. In the example, when a country is divided, the new sovereign countries inherit the richness and the trade partners of the original state.
This model is related to a previous study that enabled the production of self-similar reduced versions of complex networks, through a geometric renormalization. In these previous studies, scientists found that the connectivity in complex networks at different time scales is regulated by the same principles. “What we see in the new paper ─notes the researcher─ is that these same principles remain over time too”.
When both models are combined ─GBG and geometric renormalization─, we can create copies of the original network in a wide range of measures, larger and smaller than the original one. “This way, we could predict descendant and ascendant nodes, or study phenomena that depend on the size of the network”, highlights Serrano. “Networks present a fractal structure in time and space”, the expert adds.
These branching processes are the base of the complex evolution of many real systems. “In short, both models enable us to understand interactions in real systems at different scales, one of the keys to understand and predict what their evolution will be like”, concludes the expert.
Article reference
Muhua Zheng, Guillermo García-Pérez, Marián Boguñá, and M. Ángeles Serrano. "Scaling up real networks by geometric branchinggrowth", Proceedings of the National Academy of Sciences, May 2021. DOI: 10.1073/pnas.2018994118